Page 1 of 1
IMO shortlist 2010 G1
Posted: Mon Aug 01, 2011 3:21 pm
by sourav das
Let $ABC$ be an acute triangle with $D$;$E$;$F$ the feet of the altitudes lying on $BC$;$CA$;$AB$
respectively. One of the intersection points of the line $EF$ and the circumcircle is $P$: The
lines $BP$ and $DF$ meet at point $Q$: Prove that $AP = AQ$:
Proposed by United Kingdom
Re: IMO shortlist 2010 G1
Posted: Mon Aug 01, 2011 6:14 pm
by Tahmid Hasan
$\angle APQ=\angle BFD=\angle C$.
so quadrilateral $AFPQ$ is cyclic.\
so $\angle AFP= \angle AQP=\angle C$
hence $\angle AQP=\angle APQ $
so $AP=AQ$
Re: IMO shortlist 2010 G1
Posted: Sat Aug 13, 2011 12:05 am
by fermat's rebirth
wouldn't there be another case.................??? @Tahmid
Re: IMO shortlist 2010 G1
Posted: Wed Aug 17, 2011 11:40 am
by Tahmid Hasan
fermat's rebirth wrote:wouldn't there be another case.................??? @Tahmid
yes,i'm working on that.
Re: IMO shortlist 2010 G1
Posted: Thu Aug 25, 2011 9:01 pm
by *Mahi*
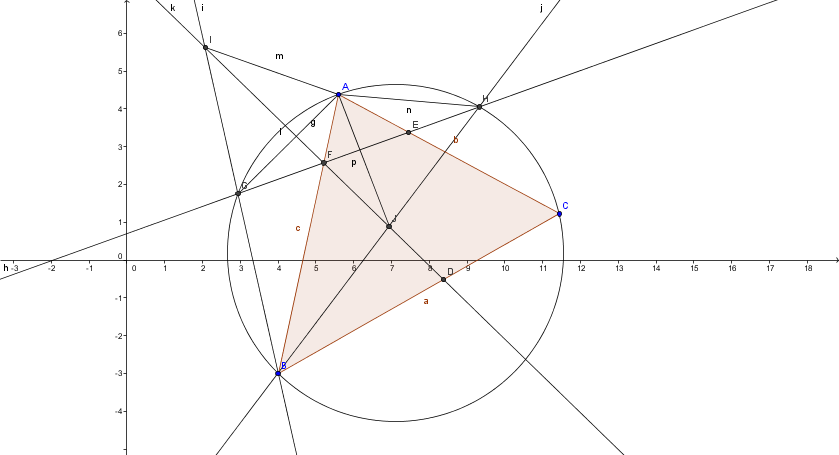
- solution 2010 G1.png (33.57KiB)Viewed 3800 times
Complete Solution:
$\angle AGB = 180 - \angle C$ So $\angle AGI =\angle C$
And $\angle AFI = \angle C $ so $AFGI$ cyclic.
So $\angle AIG =\angle C =\angle AGI$ and $AG=AI$
Again,
$\angle AHB =\angle C$ and $\angle AFD =180-\angle C$ so $AFJH$ cyclic.
Now, as $\angle AJH = \angle AFE = \angle C$, $AJ=AH$.