Let $O$ and $H$ be the circumcenter and orthocenter of $\triangle ABC$ respectively.
Let $X, Y, Z$ be the intersection point of pairs of lines $(l, l_a), (l, l_b), (l, l_c)$ respectively.
Since $l, l_a$ are reflections with respect to line $BC$, so the line $BC$ must go through $X$. Similarly, the lines $CA, AB$ goes through the points $Y,Z$ respectively.
It is a well known fact that
the reflection of the orthocenter with respect to a side of the triangle lies on the circumcircle of that triangle.
Let $D,E,F$ be the reflections of $H$ with respect to $BC, CA, AB$ repectively. So, $D,E,F$ must lie on the circumcircle of $\triangle ABC$. Also, $D,E,F$ lies on $l_a, l_b, l_c$ respectively since $H$ lies on $l$.
Let $P$ be the intersection point of pairs of lines $(l_b, l_c)$. Let $\measuredangle (l_b,l_c)$ be the directed angle mod $\pi$ that rotates the line $l_b$ to $l_c$.
Now, $\measuredangle (l_b,l_c)=\measuredangle EPF=\measuredangle YPZ=-\measuredangle PZY-\measuredangle ZYP$
$=\measuredangle YZF+\measuredangle EYZ=2(\measuredangle YZA+\measuredangle AYZ)=2\measuredangle YAZ=2\measuredangle CAB=\measuredangle EAF$.
So, $EPFA$ is a cyclic quadrilateral. So, $P$ lies on the circumcircle.
Let $Q$ be the intersection point of pairs of lines $(l_c, l_a)$. By the similar argument above, we can show that $Q$ also lies on the circumcircle.
So, $l_c$ intersects the circumcircle at $F, P, Q$. Since a line can only intersect a circle on at most $2$ distinct points, either $Q=P$ or $Q=F$.
If $Q=F$, then $l_a$ would be the line joining $F,D$. In this case, $l_a, l_b$ both has $2$ intersection points with the circle and non of them are intersection of $l_a$ and $l_b$. But this contradicts the fact that $(l_a, l_b)$ must have a intersection point on the circle.
So, it must be the case that $Q=P$. That means, $l_a, l_b, l_c$ goes through $P$ which lies on the circumcircle of $\triangle ABC$.
Q.E.D.
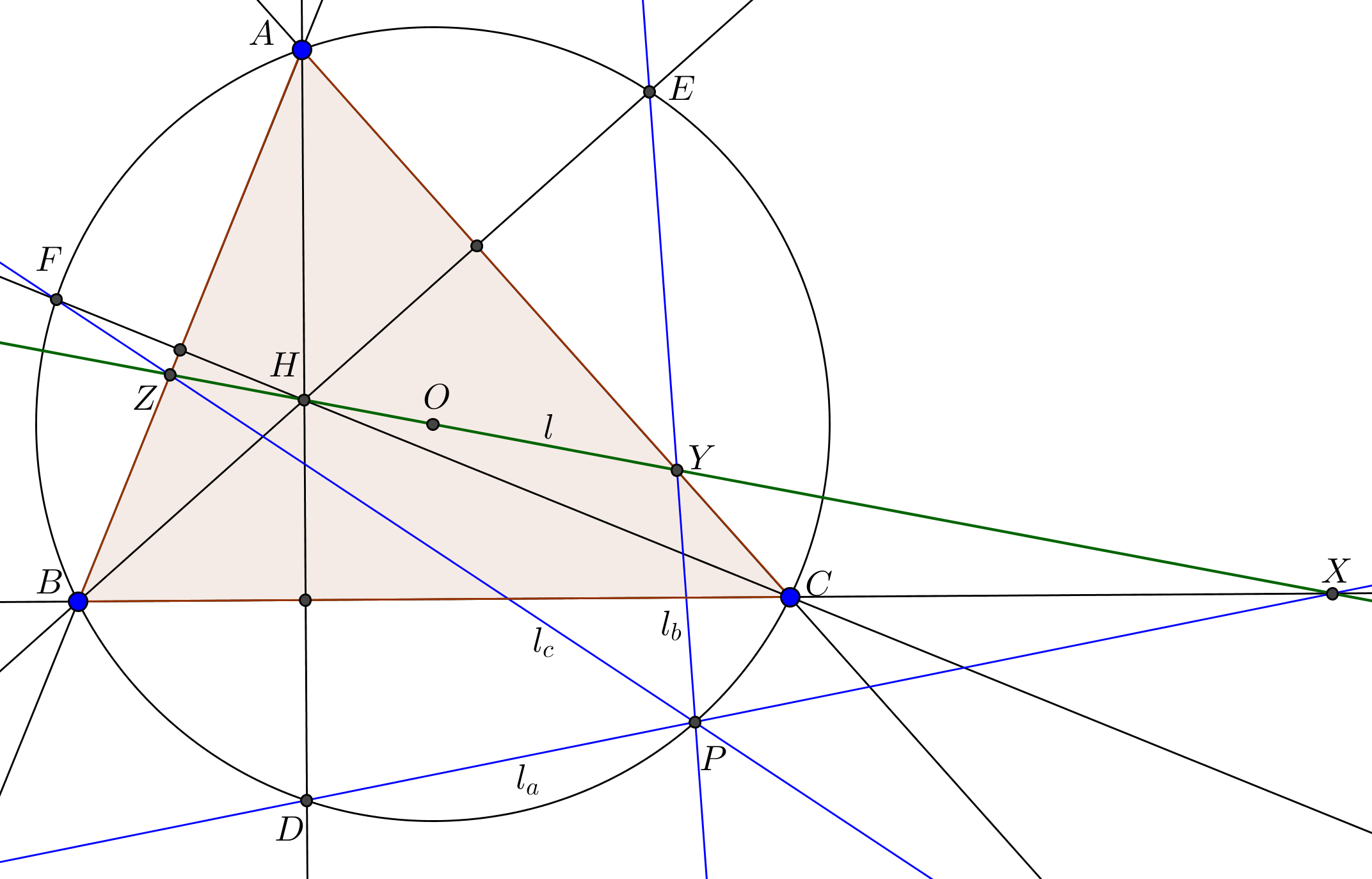
- Figure : $l_a, l_b, l_c$ are reflections of $l$ with respect to $BC, CA, AB$ respectively
- Reflection of Euler line with respect to the sides.png (180.85KiB)Viewed 9772 times